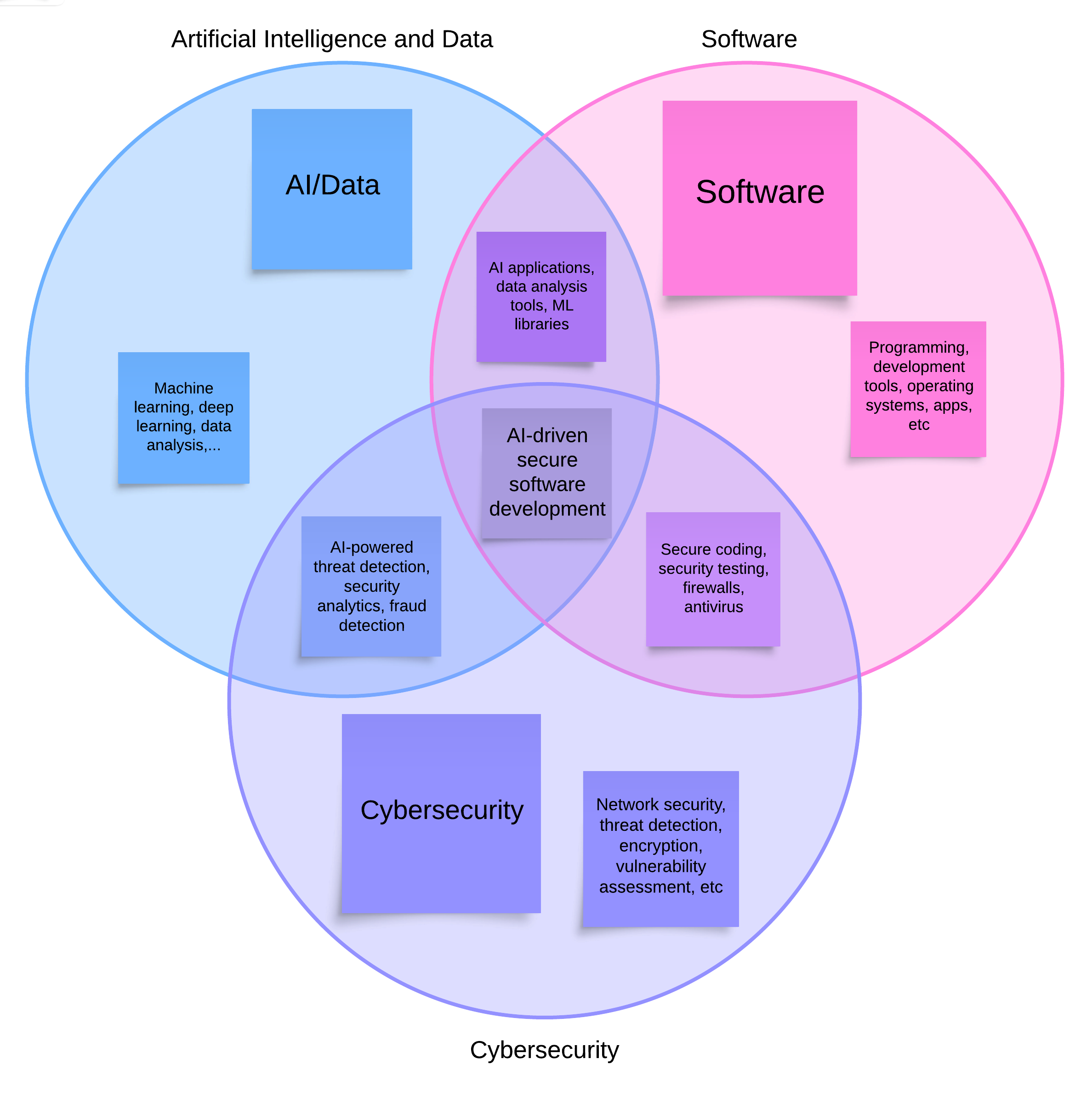
Definition
is an expression of the form:
$$ \sum_{n=1}^{\infty} a_n = a_1 + a_2 + \dots + a_i + \dots $$
The $N^{th}$partial sum $S_n$is the sum of the first N terms:
$$ S_n = a_1 + a_2 + \dots + a_N $$
We say the infinite series $\sum_{n=1}^{\infty} a_n$is convergent with sum $S$provided:
$$ S = \lim_{N \to \infty} S_N $$
if $\lim_{N \to \infty} S_N$does not exist, we say that the series diverges.
Examples
I'll provide an example of an infinite series and explain its convergence or divergence