In ordinary life
In mathematical
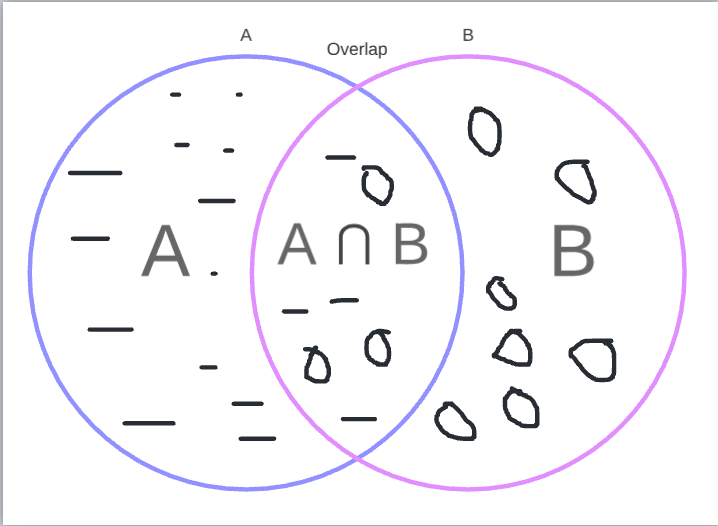
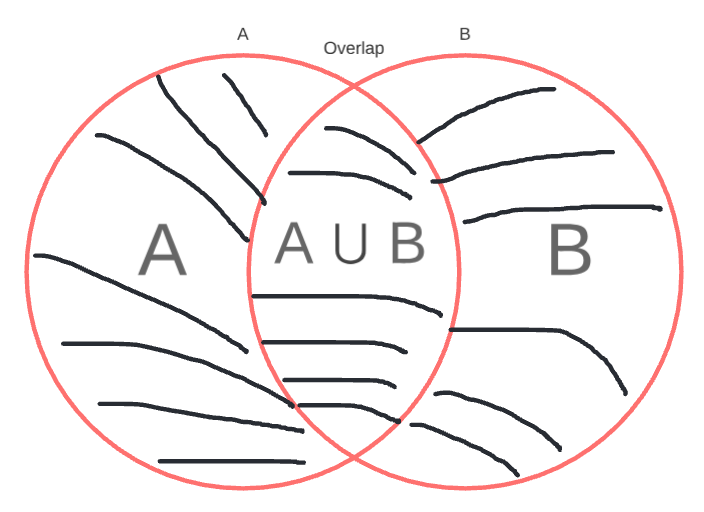
Notation
| Notation | Description | Example |
|---|---|---|
| $x \in A$ | The object $x$ is an element of the set $A$. | If $A = \{1, 2, 3\}$, $2 \in A$. |
| $x \notin A$ | The object $x$ is not an element of the set $A$. | If $A = \{1, 2, 3\}$, $4 \notin A$. |
| $\emptyset$ | The empty set, that is, the set with no elements at all. | $\emptyset = \{\}$ |
| $A \subseteq B$ | The set $A$ is contained in $B$, that’s all, every element of $A$ is also in $B$. | If $A = \{1, 2\}$ and $B = \{1, 2, 3\}$, then $A \subseteq B$. |
| $A \subset B$ | $A$ is a proper subset of $B$, meaning $A$ is contained in $B$, but they are not equal. | If $A = \{1, 2\}$ and $B = \{1, 2, 3\}$, then $A \subset B$. |
| $A \cup B$ | The union of the sets $A$ and $B$: $A \cup B = \{x \mid x \in A \text{ or } x \in B\}$. | If $A = \{1, 2\}$ and $B = \{2, 3\}$, then $A \cup B = \{1, 2, 3\}$. |
| $A \cap B$ | The intersection of the sets $A$ and $B$: $A \cap B = \{x \mid x \in A \text{ and } x \in B\}$. | If $A = \{1, 2\}$ and $B = \{2, 3\}$, then $A \cap B = \{2\}$. |
| $A \setminus B$ | The difference of the sets $A$ and $B$: $A \setminus B = \{x \mid x \in A \text{ but } x \notin B\}$ | If $A = \{1, 2\}$ and $B = \{2, 3\}$, then $A \setminus B = \{1\}$. |
Exercise: Set Operations
Let $A = \{1, 2, 3, 4\}$ and $B = \{3, 4, 5, 6\}$. Find the following:
- $$ A \cup B $$
- $$ A \cap B $$
- $$ A \setminus B $$
- $$ B \setminus A $$
- Is $A \subseteq B$?
- Is $B \subset A$?
Solutions:
- Union:
$$ A \cup B = \{x \mid x \in A \text{ or } x \in B\} $$ $$ A \cup B = \{1, 2, 3, 4, 5, 6\} $$
- Intersection:
$$ A \cap B = \{x \mid x \in A \text{ and } x \in B\} $$ $$ A \cap B = \{3, 4\} $$
- Difference (A minus B):
$$ A \setminus B = \{x \mid x \in A \text{ and } x \notin B\} $$ $$ A \setminus B = \{1, 2\} $$
- Difference (B minus A):
$$ B \setminus A = \{x \mid x \in B \text{ and } x \notin A\} $$ $$ B \setminus A = \{5, 6\} $$
- Subset Check ($A \subseteq B$):
$$ A \subseteq B \iff \forall x (x \in A \implies x \in B) $$
Since $A$ contains elements not in $B$, $A \not\subseteq B$.
- Subset Check ($B \subset A$):
$$ B \subset A \iff \forall x (x \in B \implies x \in A) $$
Since $B$ contains elements not in $A$, $B \not\subset A$.
Caution
∀: for all
∃: there exists
Another example
- The set of all integers $x$ such that $x > 5$ and $x < 3$ is the empty set: $\{x \in \mathbb{Z} \mid x > 5 \text{ and } x < 3\} = \emptyset$
- The set of all vowels in the word "rhythm" is the empty set: $\{x \mid x \text{ is a vowel in "rhythm"}\} = \emptyset$
SETS
| Set | Description |
|---|---|
| The natural numbers, $\mathbb{N}$ | The positive numbers {1, 2, 3, 4, ...}. |
| The integers, $\mathbb{Z}$ | All positive and negative numbers {..., -3, -2, -1, 0, 1, 2, 3, ...}. Keep in mind that $\mathbb{N} \subset \mathbb{Z}$. |
| The rational numbers, $\mathbb{Q}$ | These are fractions, including $\frac{1}{2}$, $-\frac{5}{4}$, 2 (since $2 = \frac{2}{1}$). We are allowed to write every integer as a fraction, $\mathbb{Z} \subset \mathbb{Q}$. |
| The real numbers, $\mathbb{R}$ | This set has all of the rational numbers, same as other digits that are unable to represented as fractions, such as $\sqrt{2}$ and $\pi$. The most effective way to think of it is to form a number line where you fill in all the gaps among rational numbers. We got this $\mathbb{Q} \subset \mathbb{R}$. |
| The complex numbers, $\mathbb{C}$ | An extension of the real digits to incorporate $\sqrt{-1}$ and same digits. |
Example: Considering that
- $\forall x \in \mathbb{Q}, 4x \in \mathbb{Z}$ $\Rightarrow$ Ex: $x = \frac{1}{3}$ $\Rightarrow$ $4x = \frac{4}{3} \notin \mathbb{Z}$ $\Rightarrow$ False
- $\exists x \in \mathbb{Q}, 4x \in \mathbb{Z}$ $\Rightarrow$ Ex: $x = \frac{1}{2}$ $\Rightarrow$ $4x = 2 \in \mathbb{Z}$ $\Rightarrow$ true
- $\forall x \in \mathbb{Z}, \frac{x}{3} \in \mathbb{Z}$ $\Rightarrow$ False
- $\exists x \in \mathbb{Z}, \frac{x}{3} \in \mathbb{Z}$ $\Rightarrow$ True
Sets of numbers
Interval notation
{ x ∈ R | 1 < x < 2} ⇒ (1,2)
{ x ∈ R | 1 <= x < 2} ⇒ [1,2)
{ x ∈ R | 1 <= x <= 2} ⇒ [1,2]
{ x ∈ R | x >= 1} ⇒ [1,∞)
Example 1:
{ x ∈ R | 0 < x <= 1} ⋂ {z ∈ R| 3z ∈ Z}
(0,1] ⋂ {……,$\frac{-1}{3}$, 0, $\frac{1}{3}$, 1, ….} = {$\frac{1}{3}$, 1}
Example 2:
{1/2, 1, 3/2, 2} ⋂ Q Z
Q = {…, $\frac{-1}{2}$, 0, $\frac{1}{2}$, 1, $\frac{3}{2}$, 2,…}
Q Z = {…, $\frac{-1}{2}$, $\frac{1}{2}$, $\frac{3}{2}$,…}
==> {1/2, 1, 3/2, 2} ⋂ {…, $\frac{-1}{2}$, $\frac{1}{2}$, $\frac{3}{2}$,…} = {$\frac{1}{2}$, $\frac{3}{2}$}
Example 3:
A = [0,4), B = {x ∈ Z | $\frac{x}{3}$ ∈ Z}, C = {kπ | k ∈ Z}
Calculate (A ∩ B) C
B = {…-6, -3, 0, 3, 6,….}
C = {....,-2π, -1π, 0, π, 2π,....}
A ∩ B = [0,4) ∩ {…-6, -3, 0, 3, 6,….} = {0, 3}
(A ∩ B) C = {0, 3} {....,-2π, -1π, 0, π, 2π,....} = {3}



Comments