Fundamental of Probability

Last updated on 17 Jan 2025

Compute Probabilities

3 things to be able to compute probabilities from an experiment:

A sample space S, at the set of results of the experiment, for example, in the coin toss experiment, the sample space S is the set of all possible outcomes: $S = \{Heads, Tails\}$
Collection of events $E \subseteq S$, for example, the same coin toss, an event E could be “getting Heads”, which is $E = \{Heads\}$. Another event could be “getting Tails”, so $E = \{Tails\}$
Function $P(E)$on the events, for instance, the probability function P(E) assigns a probability to each event. For a fair coin toss.
– P(Heads) = 0.5– P(Tails) = 0.5

Probability event

Probability Formula defines how to compute the probability of an event: $P(E) = \frac{\text{number of successes}}{\text{number of possible outcomes}}$

Example: Rolling a fair six-sided die. The sample space is $S = {1,2,3,4,5,6}$
– Let E is the event “rolling an odd number”. The event number are $\{1, 3, 5\}$, so there are 3 successful outcomes. – Total possible outcomes: 6– So the Probability is: $P(E) = \frac{3}{6} = \frac{1}{2}$

Axioms of Probability
The axioms of probability define the properties of the probability function P(E), and its function is a probability if it satisfies.

On Axioms of Probability, we have

Non-negativity: $0 \le P(E) \le 1$

The probability of any event is always between 0 and 1
Example: In a coin toss, P(Heads) = 0.5, which satisfies the axiom.

Total Probability of Sample Space P(S) = 1

The probability of the entire sample space is always 1, as one of the possible outcomes must occur.
Example: In a six-sided die roll, $P(S) = P(\{1,2,3,4,5,6\}) = 1$, as there is no chance of the die showing a result outside the set.
The way to get P(S) = 1, is the entire sample space S is the sum of the probabilities of individual outcomes: $P(S) = P(\{1,2,3,4,5,6\}) = P(1) + P(2) + P(3) + P(4) + P(5) + P(6) $

Sum the probabilities of each outcome:

$$ P(S) = \underbrace{\frac{1}{6} + \dots + \frac{1}{6}}_{\text{plus together six times as 6-sided}} = 1 $$

Additivity for Disjoint Events: If $E_1, E_2, \dots$are disjoint (mutually exclusive) events, then:

$P(E_1 \cup E_2 \cup \dots) = \sum_{i=1}^\infty P(E_i)$and $E_i \cap E_j = \cancel{0}$if $i \neq j$:

Example: Consider rolling a six-sided die. Let $E_1 = \{1,2\}$and $E_2 = \{3,4\}$. These events are disjoint.

$$ P(E_1) = \frac{2}{6} = \frac{1}{3} $$ $$ P(E_2) = \frac{2}{6} = \frac{1}{3} $$ $$ P(E_1 \cup E_2) = P(E_1) + P(E_2)= \frac{1}{3} + \frac{1}{3}= \frac{2}{3} $$

Example

What is the probability of rolling a 5 in Monopoly (two dice, total dice calculation)?

$$ S = 6 \cdot 6 = 36 $$ $$ E = (1, 4), (4, 1), (2, 3), (3, 2) = 4 $$ $$ P(E) = \frac{4}{36} = \frac{1}{9} $$

If 4 balls are drawn from a ball (with replacement) containing 7 red and 4 green balls, what is the probability that 2 ball is red and 2 are green

Draw 4 balls, 7 red, 4 green. P(2red, 2green), P(RRGG), P(RGRG), P(RGGR), P(GRRG), P(GRGR), P(GGRR)

Use Axioms of Probability, we have:

The set of all possible outcomes of an experiment - Sample Space: $S = 11$, which represent total number of balls (7R + 4G)

The outcome of interest, event: $E = 4$, which refer to the event of drawing 4 balls (with replacement)

Probabilities of drawing a red ball (P(Red)): $P(Red) = \frac{7}{11}$

Probabilities of drawing a green ball (P(Green)): $P(Green) = \frac{4}{11}$

Calculate the probabilities of 2Red and 2Green: P(2R, 2G): $\frac{7}{11} \cdot \frac{7}{11} \cdot \frac{4}{11} \cdot \frac{4}{11} = \frac{784}{14641}$

Combination with repetition:

The probability of getting exactly k balls given in number of successes $\binom{4}{2} = \frac{4!}{2!(4-2)!} = \frac{4 \times 3}{2 \times 1} = 6$

Permutation of 2 red and 2 green:

$$ \binom{4}{2} \cdot \binom{7}{11}^2 \cdot \binom{4}{11}^2 = 6 \cdot \frac{784}{14641} = \frac{4704}{14641} \approx 0.321 $$

Complement Rule

Call $E^c$is the complement of event E $P(E) + P(E^c) = 1$

Explain: The probability of an event E plus the probability of its complement $E^c$ is always equal to 1:

Example

Suppose that there is a 30% chance of rain tomorrow.
The complement is the chance it will not rain.
Event P(rain) = 0.3, so the complement P(No Rain) = $1 -0.3 = 0.7$

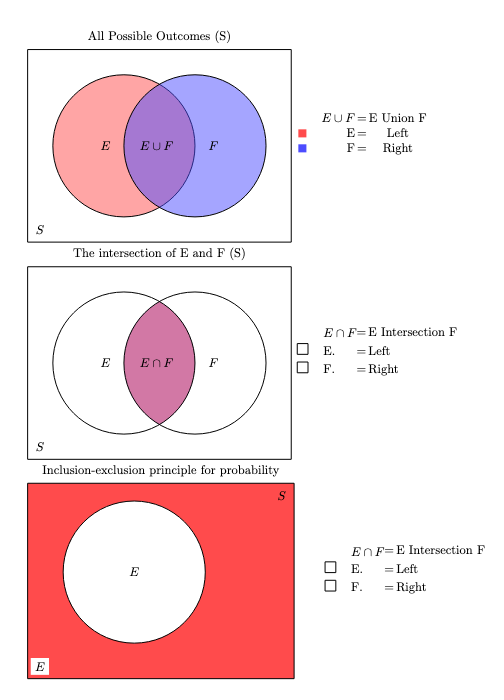
The inclusion-exclusion principle for probabilities is:
$$ P(E \cup F) = P(E) + P(F) - P(E \cap F) $$

Example:

Make E be the event of “a student studies math” with P(E) = 0.6
Make F be the event of “a student studies physics” with P(F) = 0.4
Let $P(E \cap F) = 0.2$(students studying both)
$P(E \cup F) = 0.6 + 0.4 - 0.2 = 0.8$(student studies either math or physics or both)