y = f(x), Domain: D
$$ f(x) = \sqrt{x+2}, D = x + 2 \ge 0 \leftrightarrow x \ge -2 $$
D(f) = [2, inf]
Polynomials
$$ p(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0 $$
For example
| Type of Polynomials | Degree | Definition | Example |
|---|---|---|---|
| Constant | 0 | simply a constant term. | $f(x) = 5$ |
| Linear | 1 | represents a straight line | $ f(x) = 2x - 3$ |
| Quadratic | 2 | represents a parabola | $f(x) = x^2 + 4x + 1$ |
| Cubic | 3 | $f(x) = 3x^3 - 2x^2 + x + 7$ | |
| Quartic | 4 | $f(x) = x^4 + 7x^3 - 2x + 1$ | |
| Quintic | 5 | $f(x) = 2x^5 - x^3 + 4x - 9$ |
Rational functions
If $p(x)$and $q(x)$ are polynomial functions, there is the form of rational function r(x): $r(x) = \frac{p(x)}{q(x)}$
The domain of $r(x)$ is $\mathcal{D} = \{x \mid q(x) \neq 0\}$
Example
Simple Rational Function
- $$ r(x) = \frac{x + 2}{x - 3} $$
p(x) = x + 2 (a linear polynomial)
q(x) = x - 3 (another linear polynomial)
Domain: All real numbers except x = 3 (since q(3) = 0), also called: $\mathcal{D} = \{x \in R \mid x \neq 3\}$
- $$ r(x) = \frac{x^2 - 4}{x^2 + 2x + 1} $$
p(x) = $x^2 - 4$ (a quadratic polynomial)
q(x) = $x^2 + 2x + 1$ (another quadratic polynomial)
Domain: All real numbers except x = -1 (since q(-1) = 0), also called:$\mathcal{D} = \{x \in R \mid x \neq -1\}$
- $$ r(x) = \frac{2x^3 - 5x + 1}{x^3 - 8} $$
p(x) = 2x^3 - 5x + 1 (a cubic polynomial)
q(x) = x^3 - 8 (another cubic polynomial)
Domain: All real numbers except x = 2 (since q(2) = 0), also called: $\mathcal{D} = \{x \in R \mid x \neq 2\}$
Absolute value function
This function $f(x) = \lvert x \rvert$ is defined by the rule of two-part:
$$ f(x) = \lvert x \rvert = \begin{cases} x & \text{if } x \ge 0, \\ -x & \text{if } x < 0 \end{cases} $$
Domain D = R, the range is $\{x \mid x \ge 0\} = [0, \infty)$
Examples
f(3) = |3| = 3 (Because 3 is positive, the absolute value is always 3)
f(-3) = |-3| = 3 (Because -3 is negative, the absolute value changes to its positive counterpart, 3)
f(0) = |0| = 0 (The absolute value of 0 is 0)
Piecewise functions
This allow to change intervals, like $\le \text to <$, but to make sure that should not overlap.
$$ f(x) = \begin{cases} x & \text{if } x \le 0, \\ -x & \text{if } 0 < x \le 1, \\ 1 & \text{if } x > 1 \end{cases} $$
Examples
f(x) =
f(-2), $-2 \le 0 $, apply the first part of the definition: f(-2) = -2
f(0.5), $0 < 0.5 \le 1$, apply the second part of the definition: f(0.5) = -0.5
f(1), $0 < 1 \le 1$, apply the second part of the definition: f(1) = 1
f(3), $3 > 1$, apply the third part of the definition f(3) = 3
Another one with piecewise functions
2x if x < 0
3x if $0 \le x < 2$
4x if $2 \le x < 4$
5x if $x \ge 4$
f(x) =
f(-2), $-2 \le 0 $, apply the first part of the definition: f(-2) = $-2 * 2 = -4$
f(0.5), $0 < 0.5 \le 2$, apply the second part of the definition: f(0.5) = $0.5 * 3 = 1.5$
f(1), $0 \le 1 < 2$, apply the second part of the definition: f(1) = $1 * 4 = 4$
f(3), $2 \le 3 < 4$, apply the third part of the definition f(3) = $3 * 4 = 12$
f(4), $4 \ge 4$, apply the third part of the definition f(3) = $4*5=20$
Another one (not N and N)
f(x) =
$\frac{-17}{4}x$ if x < 0
0.5x if 0 ≤ x < 2
2x if 2 ≤ x < 4
$\frac{17}{4}x$ if x ≥ 4
f(x) =
f(-2), $-2 \le 0 $, apply the first part of the definition: f(-2) = $-2 * \frac{17}{4} = -\frac{17}{2}$
f(0.5), $0 \le 0.5 < 2$, apply the second part of the definition: f(0.5) = $0.5 * 0.5 = 0.25$
f(1), $0 \le 0.5 < 2$, apply the second part of the definition: f(1) = $1 * 0.5 = 0.5$
f(3), $2 \le 3 < 4$, apply the third part of the definition f(3) = $3 * 2 = 6$
f(4), $4 \ge 4$, apply the third part of the definition f(3) = $4*\frac{17}{4}=17$
Calculate domains of r(x), where r(x) =
$$ \frac{3x^4 - 5x^2 + 3x - 1}{x^3 - x} $$
We check on denominator $x^3 - x \neq 0$
$$ x(x^2 - 1) \neq 0 $$ $$ \begin{cases} x = 0 \\ x^2 - 1 = 0 \end{cases} $$ $$ Two \space conditions => \begin{cases} x = 0 \\ x^2 = \pm1 \end{cases} $$
$D(r) = (-\infty, -1) \space \cup \space (0, 1) \space \cup \space (1, +\infty)$ OR $D(r) = R \space \setminus \space \{-1, 0, 1\}$
Draw the graph of functions
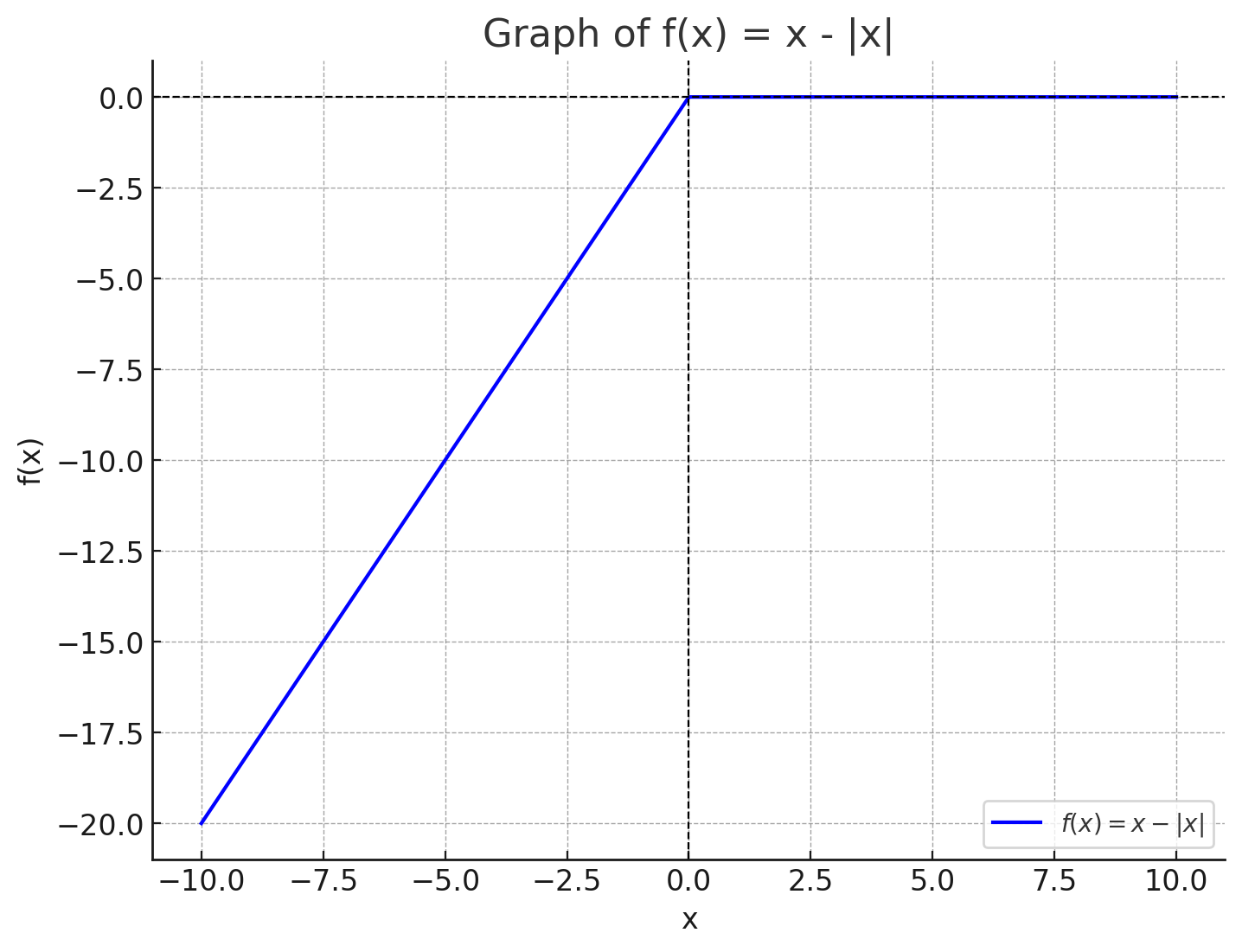
$$ f(x) = x - |x| $$
Case 1: if $x \ge 0$
- So, the absolute value of x is $|x| = x$
- Substituting into the function: x - x = 0
Case 2: if $x < 0$
- So, the absolute value of x is $|x| = -x$
- Substituting into the function: x - (-x) = 2x
So, the function, therefore, will shows as pre-wise function:
$$ f(x) = \begin{cases} 0 & \text{if } x \ge 0, \\ 2x & \text{if } x < 0 \end{cases} $$
Build a new function from old functions
| Name | variable | formula |
|---|---|---|
| the sum | $f + q$ | $(f + q)(x) = f(x) + g(x)$ |
| difference | $f - q$ | $(f-g)(x) = f(x) - g(x)$ |
| product | $f \cdot g$ | $(f \cdot g)(x) = f(x)g(x)$ |
| quotient | $\frac{f}{g}$ | $\frac{f}{g} (x) = \frac{f(x)}{g(x)}$ |
Definition: Composition of functions:
Given any of the two functions in f and g: $(f \circ g)(x) = f(g(x)) \space and \space (g \circ f)(x) = g(f(x))$
f(g(x)) is g(x) is nested at f(x)
g(f(x)) is vice versa above
The composition $f \circ g $ has domain $\{ x \in \mathcal{D}(g) \mid g(x) \in \mathcal{D}(f) \}$
Example
We have f(x) = 2x, g(x) = $x^2$
Make the table from new functions:
| Name | variable | new functions |
|---|---|---|
| the sum | $f + q$ | $(f + q)(x) = 2x + x^2$ |
| difference | $f - q$ | $(f-g)(x) = 2x - x^2$ |
| product | $f \cdot g$ | $(f \cdot g)(x) = 2x \cdot x^2 = 2x^3$ |
| quotient | $\frac{f}{g} $ | $\frac{f}{g} (x) = \frac{2x}{x^2} = \frac{2}{x}$ |
Composition of functions:
| Function | New function |
|---|---|
| $(f \circ g)(x) = f(g(x))$ | $f(x) = 2(x^2) = 2x^2$ |
| $(g \circ f)(x) = g(f(x))$ | $f(x) = (2x)^2 = 4x^2$ |
Example: Build a new function from old function
Example: $f(x) = \sqrt{x + 1}, \ g(x) = \sqrt{5 - x}$
$$ D(f) = [-1, +\infty); \space D(g) = [5, +\infty) $$
Make the table to calculate $f(x) + g(x), f(x) - g(x), f(x) \circ g(x), \frac{f(x)}{g(x)}$and their domains
Domains:
$\sqrt{x + 1}$, we need to put at condition at: $x + 1 \ge 0 <=> x \ge -1$, means that x can take any value at: $[-1, +\infty)$
$\sqrt{5 - x}$, we need to put at condition at: $5 -x \ge 0 <=> x \le 5$
means that x can take any value at: $(-\infty, 5]$
Combined domain:
f(x) and g(x) is the intersection of D(f) and D(g), which is:
$$ D(f) \cap D(g) = [-1, 5] $$
| Function | New function | Domain |
|---|---|---|
| $f(x) + g(x)$ | $(\sqrt{x + 1}) + (\sqrt{5 - x})$ | $[-1, 5]$ |
| $f(x) - g(x)$ | $(\sqrt{x + 1}) - (\sqrt{5 - x})$ | $[-1, 5]$ |
| $f(x) \circ g(x)$ | $(\sqrt{x + 1}) \circ (\sqrt{5 - x})$ | $[-1, 5]$ |
| $\frac{f(x)}{g(x)}$ | $\frac{\sqrt{x + 1}}{\sqrt{5 - x}}$ | $[-1, 5)$ |
Composition:
| Function | New function | Domain |
|---|---|---|
| $(f \circ g)(x) = f(g(x))$ | $f(x) = \sqrt{\sqrt{5 - x} + 1}$ | $\sqrt{5 - x} + 1 \ge 0 \\ \Leftrightarrow x \le 5$ |
| $(g \circ f)(x) = g(f(x))$ | $f(x) = \sqrt{5 - \sqrt{x + 1}}$ | $5 - \sqrt{x + 1} \ge 0 \Leftrightarrow x \in [-1, 24]$ |
Another example on build a new function from old functions
$f(x) = x^2, g(x) = \sqrt{x+2}$, find $(f \circ g)(x)$, and find $(g \circ f)(x)$, and domains
$$ (f \circ g)(x) = f(g(x)) = (\sqrt{x+2})^2 = x + 2 ; D(f \circ g) = [-2, +\infty) $$ $$ (g \circ f)(x) = g(f(x)) = \sqrt{x^2 + 2}; D(g \circ f) = R $$
More example….
$f(x) = \frac{1}{x}, g(x) = sin(x)$, find $(f \circ g)(x)$and find $(g \circ f)(x)$, and domains
$$ (f \circ g)(x) = f(g(x)) = \frac{1}{\sin(x)}; \ D(f \circ g) = \mathbb{R} \setminus \{ \ldots, -4\pi, -2\pi, 0, 2\pi, 4\pi, \ldots \} $$ $$ (g \circ f)(x) = g(f(x)) = sin(\frac{1}{x}); D(g \circ f) = \mathbb{R} \setminus \{0\} $$
Find inverse of
$f(x) = 2x + 4$, and $f(x) = \frac{7x+3}{x-1}$
Replace $f(x) \implies y$
- For $f(x) = 2x + 4 \leftrightarrow y = 2x +4 \leftrightarrow x = 2y +4 \leftrightarrow 2y = x - 4 $
$$ \leftrightarrow y = \frac{x-4}{2} \leftrightarrow f^{-1}(x) = \frac{x-4}{2} $$
- For $f(x) = \frac{7x+3}{x-1} \leftrightarrow y = \frac{7x+3}{x-1} \leftrightarrow x = \frac{7y+3}{y-1} \leftrightarrow x(y-1) = 7y+3 $
$$ \leftrightarrow xy - x = 7y + 3 \leftrightarrow xy - 7y = x +3 \leftrightarrow y(x - 7) = x +3 \leftrightarrow y = \frac{x + 3} {x - 7} \leftrightarrow f^{-1}(x) = \frac{x + 3} {x - 7} $$



Comments